ESKF笔记
ESKF(error-state Kalman Filter)
Reference
贝叶斯滤波
首先确定存在系统方程:xk=f(xk−1,uk,wk)
以及观测方程:yk=h(xk,vk)
其中,x表示系统状态,y表示观测量,w表示系统传递噪声,v表示观测误差。
四元数
- 表示形式
Q=a+bi+cj+dk
q = q w + qv
q=[qw qv] - 四元数的乘法运算,可以写作矩阵计算的形式
- 通过四元数的微分方程 q ˙ = q ⊗ Ω \dot q=q \otimes \Omega q˙=q⊗Ω可以看到,四元数与SO(3)一样,可以写作exp映射的形式,并且,两者的旋转向量是一样的,不过对于旋转矩阵的映射而言,首先会将旋转向量映射到so(3)上,之后SO(3)与so(3)通过exp来一一对应,而四元数是将旋转向量先映射到切线空间之后再与四元数进行exp映射
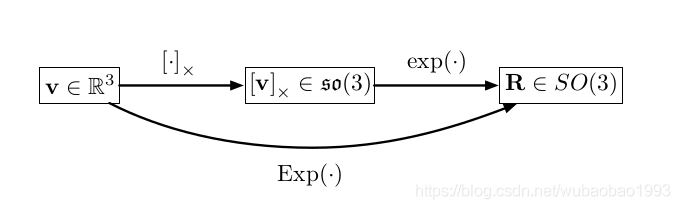
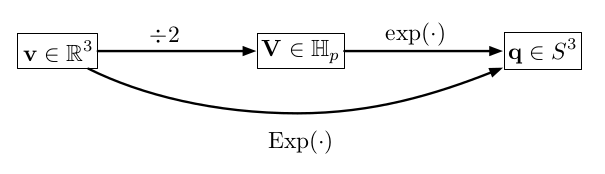
其中SO3是指三维特殊正交群,so3是指三维特殊正交群的李代数
支持李群和李代数运算的库文件是Sophs,支持SO(3),so(3),SE(3)和se(3)的定义和运算,继承于Eigen,所以可以使用Eigen定义的类和函数。
1 | 三维旋转群SO3:Sophus::SO3 |
Sophus库转换关系图
ESKF
这里稍微解释一下误差方程,由于在做IMU的解算时,做了一些近似,而那些舍掉的东西就给IMU解算带来了误差。ESKF要做的就是对误差进行滤波,获得当前情况下误差的最优估计,然后将计算出来的位移、速度、姿态等量减去这个误差,修正由于近似带来的不准确。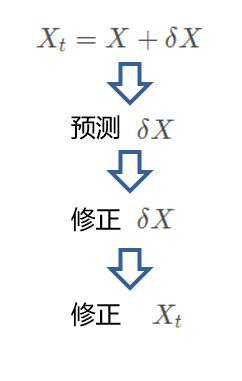
基本KF

万向锁问题
万向锁(Gimbal lock): 一旦选择±90°作为pitch角,就会导致第一次旋转和第三次旋转等价,整个旋转表示系统被限制在只能绕竖直轴旋转,丢失了一个表示维度。
对于万向锁的问题,只有在动态欧拉角中出现,而静态欧拉角不存在万向锁的问题!!!
静态: 即绕世界坐标系三个轴的旋转,由于物体旋转过程中坐标轴保持静止,所以称为静态,此时各个变换顺序的旋转矩阵是左乘的
动态: 即绕物体坐标系三个轴的旋转,由于物体旋转过程中坐标轴随着物体做相同的转动,所以称为动态,此时各个变换顺序的旋转矩阵是右乘的
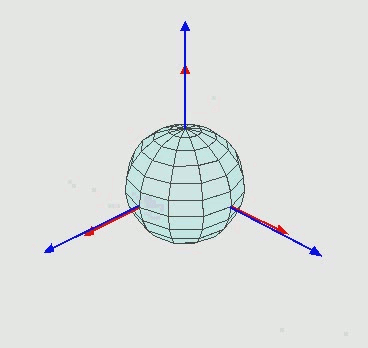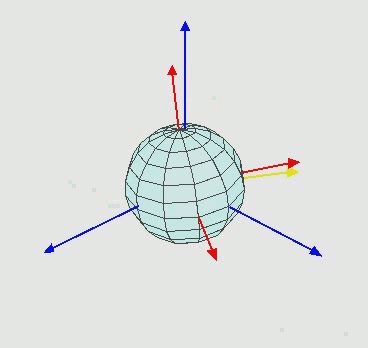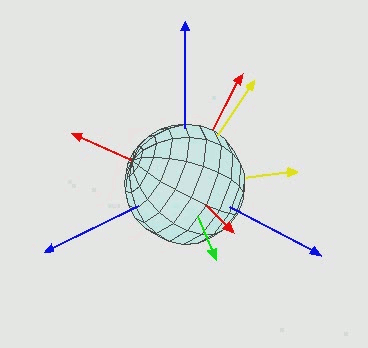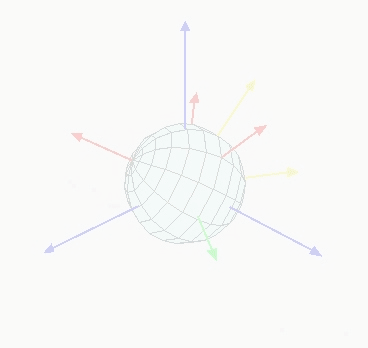
内旋Intrinsic rotations:绕运动轴
外旋 Extrinsic rotations: 绕固定轴
formula
Predict
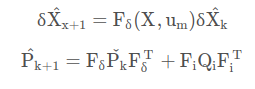
Update

预积分
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Wizard!

